In learning an embodied agent executing daily tasks via language directives, the literature largely assumes that the agent learns all training data at the beginning. We argue that such a learning scenario is less realistic since a robotic agent is supposed to learn the world continuously as it explores and perceives it. To take a step towards a more realistic embodied agent learning scenario, we propose two continual learning setups for embodied agents; learning new behaviors (Behavior Incremental Learning, Behavior-IL) and new environments (Environment Incremental Learning, Environment-IL). For the tasks, previous ‘data prior’ based continual learning methods maintain logits for the past tasks. However, the stored information is often insufficiently learned information and requires task boundary information, which might not always be available. Here, we propose to update them based on confidence scores without task boundary information during training (i.e., task-free) in a moving average fashion, named Confidence-Aware Moving Average (CAMA). In the proposed Behavior-IL and Environment-IL setups, our simple CAMA outperforms prior state of the art in our empirical validations by noticeable margins.
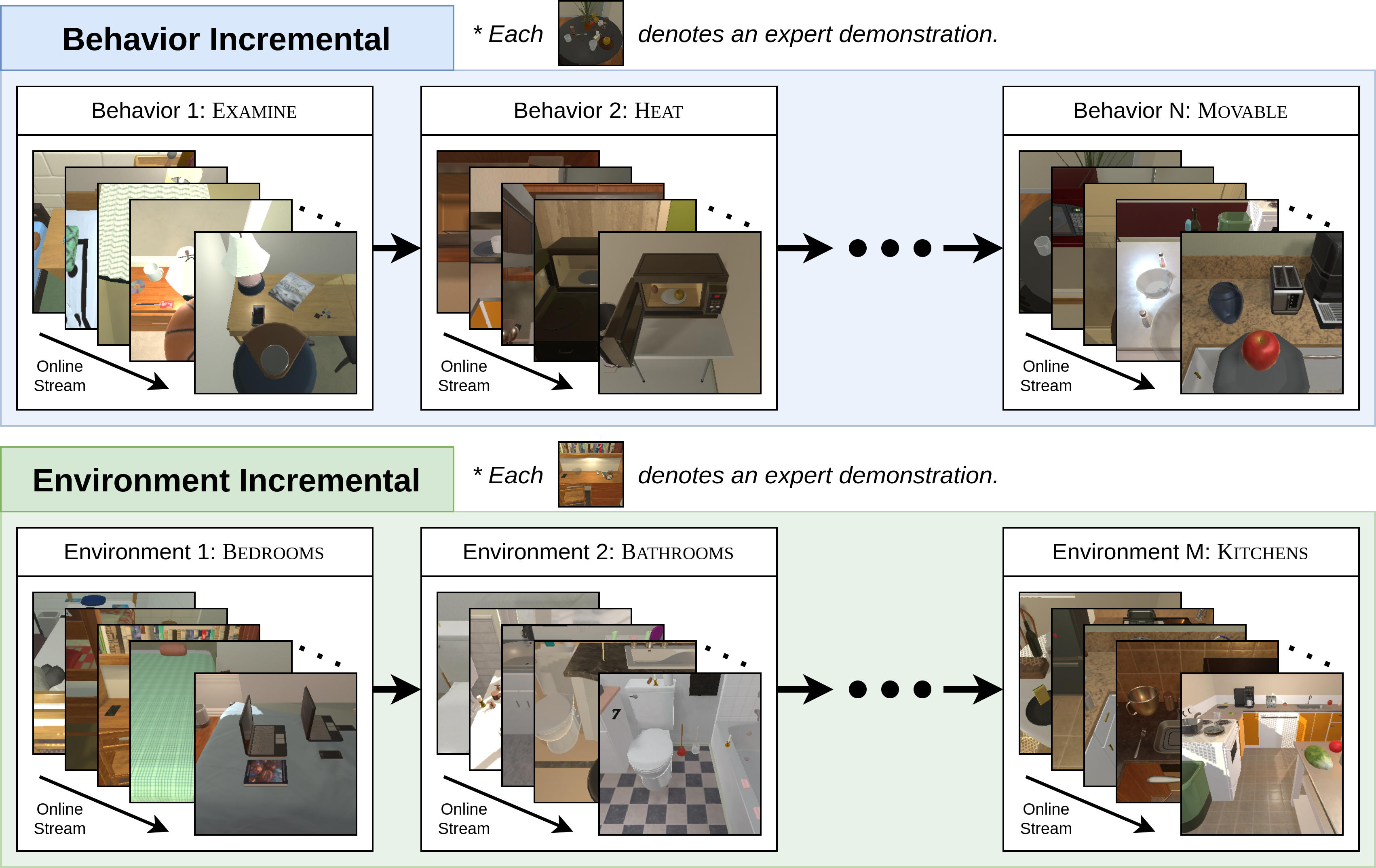
Continual learning enables agents to adapt to new behaviors and diverse environments after deployment, mitigating the risk of forgetting previously acquired knowledge. To foster active research on mitigating catastrophic forgetting and comprehensively address the combined challenges of continuous learning of an agent with natural language understanding and object localization, we use full-fledged interactive instruction following tasks and propose two incremental learning setups, Behavior Incremental Learning (Behavior-IL) and Environment Incremental Learning (Environment-IL).
Behaviors described by instructions may exhibit considerable diversity as novel behaviors may arise over time. To address this scenario, we propose the Behavior-IL setup that facilitates the agent’s incremental learning of new behaviors while retaining knowledge obtained from previous tasks.
We adopt seven different types of behavior from ALFRED: EXAMINE, HEAT, COOL, CLEAN, PICK&PLACE, PICK2&PLACE, and MOVABLE. For the agent's adaptability and avoid favoring particular behavior sequences, we train and evaluate agents using multiple randomly ordered behavior sequences.
The Environment-IL setup allows agents to incrementally learn novel environments. In the real world, agents often need to perform actions not only in the environment in which they were initially trained but also in new and different environments that are presented.
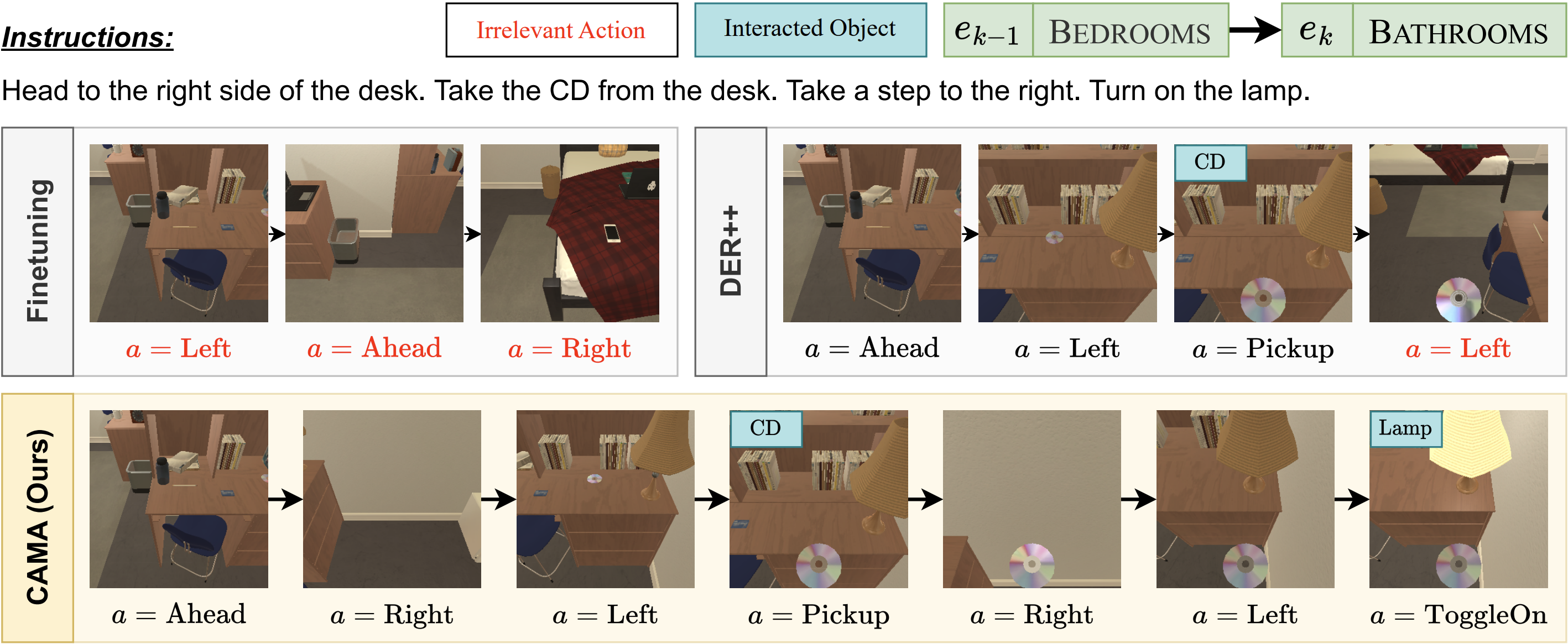
In this setup, we adopt four different types of environments supported by AI2-THOR: KITCHENS, LIVINGROOMS, BEDROOMS, and BATHROOMS. Like the Behavior-IL setup, we conduct training and evaluation using multiple sequences of randomly ordered environments.
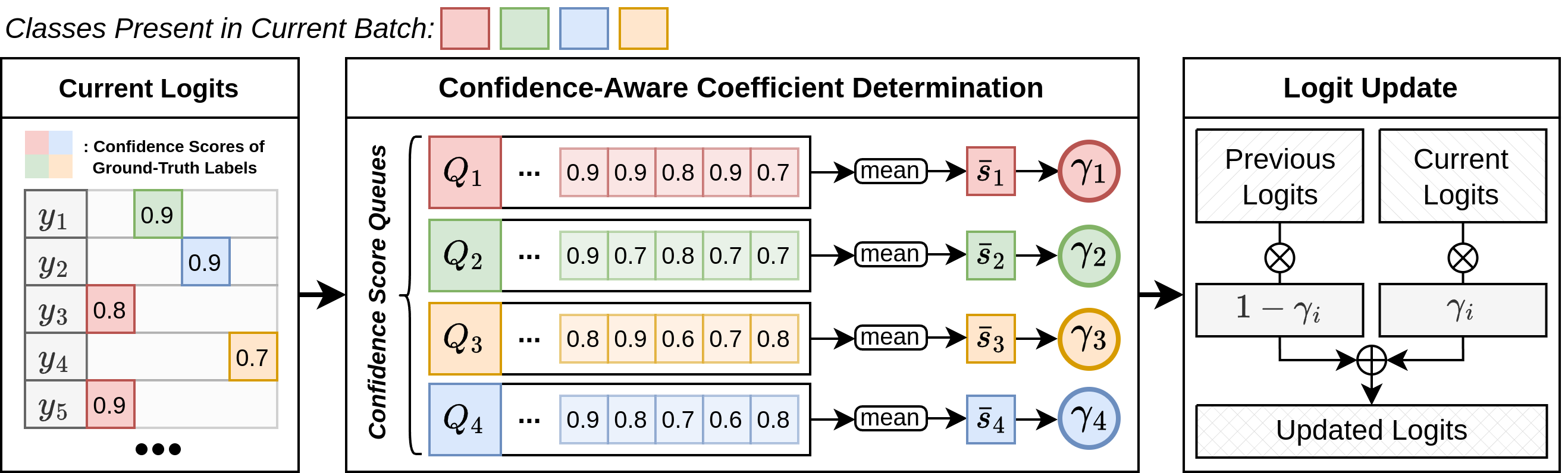
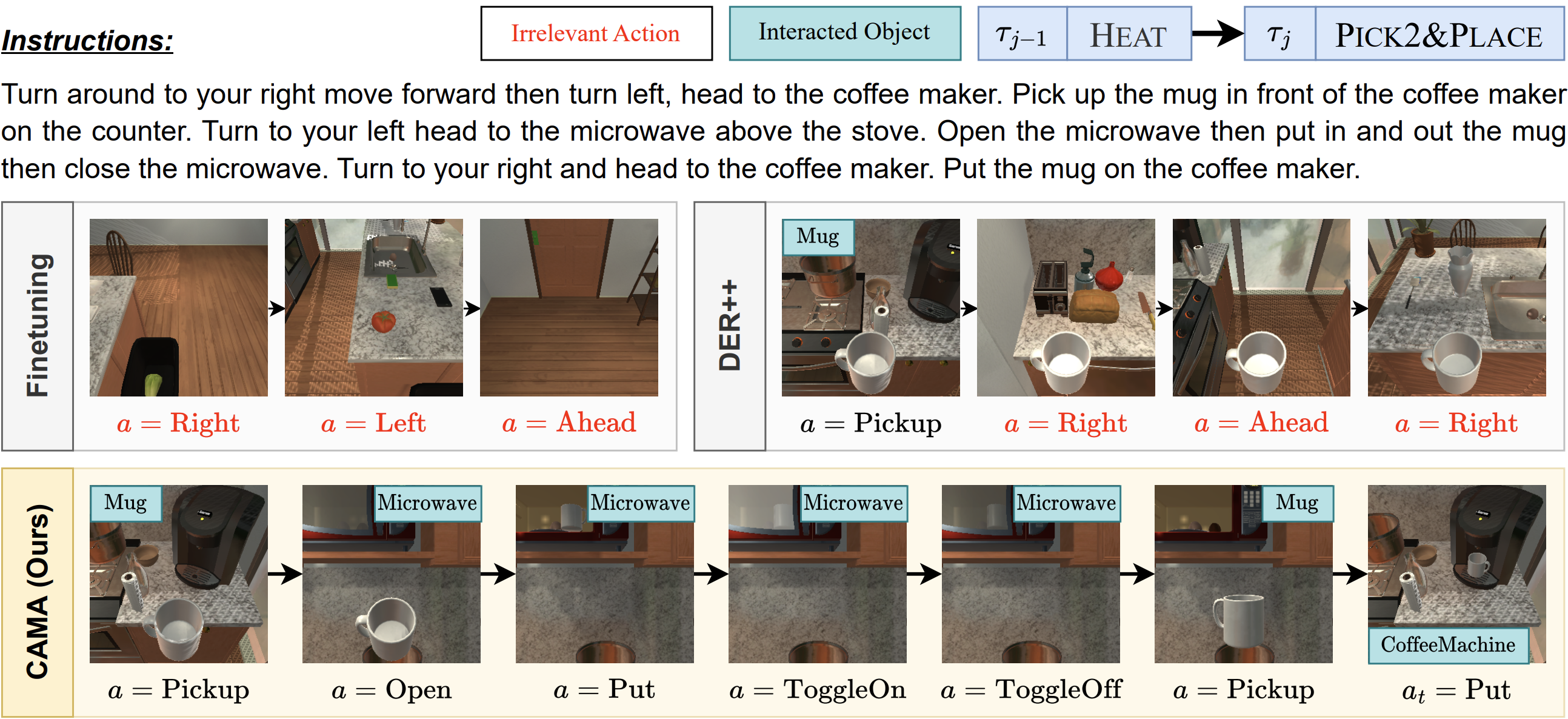
To mitigate catastrophic forgetting, recent approaches use knowledge distillation with trained models or logits until past tasks, but this often entails significant memory and computational cost by additional model inference or outdated logit problems due to no updates on past logits. To address this issue, we propose CAMA (Confidence-Aware Moving Average) to update the stored logits using the agent's confidence scores indicating how the newly obtained logits for update contain accurate knowledge of the corresponding tasks.
First, we construct an input batch, \([x; x']\), by combining data from both the training data stream \((x, y_a, y_c)\sim\mathcal{D}\) and the episodic memory \((x', y'_a, y'_c, z'_{old,a}, z'_{old,c})\sim\mathcal{M}\), where each \(a \in \mathcal{A}\) and \(c \in \mathcal{C}\) indicates an action and object class label from the action and object class sets, \(\mathcal{A}\) and \(\mathcal{C}\), present in the input batch, \([x; x']\). Here, \(x\) represents the input (i.e., images and language directives), \(y_a\) and \(y_c\) denote the corresponding action and object class labels, and \(z'_{old,a}\) and \(z'_{old,c}\) refers to the corresponding stored logits. \(z_a\), \(z_c\), \(z'_a\), and \(z'_c\) denote the current model's logits for the input batch.
To prevent the logits maintained in the episodic memory from becoming outdated, we obtain the updated logits, \(z'_{new,a}\) and \(z'_{new,c}\), by weighted-summing \(z'_{old,a}\) and \(z'_{old,c}\) with \(z'_{a}\) and \(z'_{c}\) using coefficient vectors, \(\gamma_a\) and \(\gamma_c\), using Hadamard product, denoted by \(\odot\): \begin{equation} \label{eq:weighted_sum} z'_{new,a} = (\mathbf{1} - \gamma_a) \odot z'_{old,a} + \gamma_a \odot z'_a, ~~~ z'_{new,c} = (\mathbf{1} - \gamma_c) \odot z'_{new,c} + \gamma_c \odot z'_c. \end{equation}
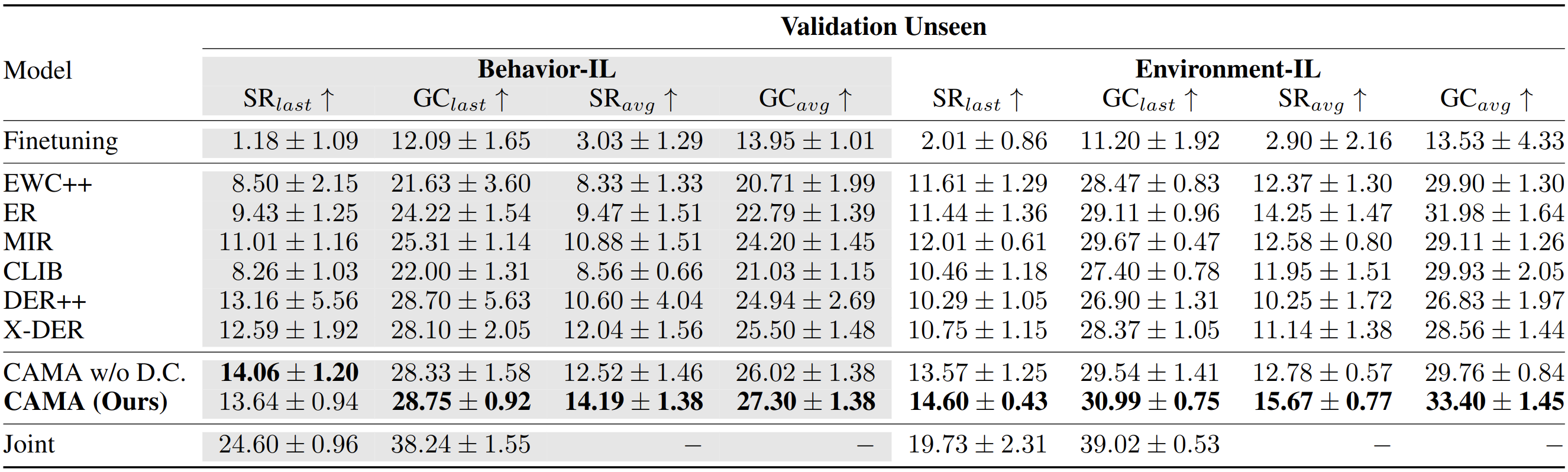
To obtain \(\gamma_a\) and \(\gamma_c\), we first maintain the most recent \(N\) confidence scores for each action and object class label for \(x\). Then, to approximate the agent's proficiency in learning tasks over time, we compute the average of the scores associated with each action (\(i\)) and object class (\(j\)) label, denoted by \(\bar{s}^a_i\) and \(\bar{s}^c_j\). We then set each element of \(\gamma_a\) and \(\gamma_c\), denoted by \(\gamma_{a,i}\) and \(\gamma_{c,j}\), to \(\bar{s}^a_i\) and \(\bar{s}^c_j\) followed by a CLIP function as: \begin{equation} \label{eq:mean_confidence_score} \begin{split} \gamma_{a,i} = \alpha_a \text{CLIP} \left( \bar{s}^a_i - |\mathcal{A}|^{-1}, 0, 1 \right), ~~~ \gamma_{c,j} = \alpha_c \text{CLIP} \left( \bar{s}^c_j - |\mathcal{C}|^{-1}, 0, 1 \right), \end{split} \end{equation} where \(\text{CLIP}(x, \min, \max)\) denotes the clip function that limits the value of \(x\) from \(\min\) to \(\max\). Here, the constants \(\alpha_a < 1\) and \(\alpha_c < 1\) are introduced to prevent \(\gamma_{a,i}\) and \(\gamma_{c,j}\) from reaching a value of 1 as this indicates complete replacement of the prior logits with the current logits, which implies that the updated logits would entirely forget the previously learned knowledge. The inclusion of these constants ensures that some information from the past is retained and not entirely overridden by the current logits during the update process. In addition, we subtract \(|\mathcal{A}|^{-1}\) and \(|\mathcal{C}|^{-1}\) enhances the effective utilization of confidence scores in comparison to a `random' selection, which would otherwise be realized by a uniform distribution.We follow the same evaluation protocol of ALFRED. The primary metric is the success rate (SR) which measures the ratio of the succeeded episodes among the total ones. The second metric is the goal-condition success rate (GC) which measures the ratio of the satisfied goal conditions among the total ones. Furthermore, we evaluated all agents in two splits of environments: seen and unseen environments which are/are not used to train agents.
To evaluate the last and intermediate performance of continual learning agents, we measure two variations of a metric, \(A\): \(A_{last}\) and \(A_{avg}\). \(A_{last}\) (here, \(\text{SR}_{last}\) and \(\text{GC}_{last}\)) indicates the metric achieved by the agent that finishes its training for the final task. \(A_{avg}\) (here, \(\text{SR}_{avg}\) and \(\text{GC}_{avg}\)) indicates the average of the metrics achieved by the agents that finish their training for each incremental task.
For more details, please check out the paper.
@inproceedings{kim2024online,
author = {Kim, Byeonghwi and Seo, Minhyuk and Choi, Jonghyun},
title = {Online Continual Learning for Interactive Instruction Following Agents},
booktitle = {ICLR},
year = {2024},
}